Vitalik : Binius, des preuves efficaces pour les champs binaires

Article original de : Vitalik Buterin

Traduction originale : Kate, MarsBit

Cet article s'adresse principalement aux lecteurs qui sont généralement familiers avec la cryptographie de l'ère 2019, et en particulier avec les SNARK et les STARK. Si ce n’est pas le cas, je vous recommande de les lire en premier. Un merci spécial à Justin Drake, Jim Posen, Benjamin Diamond et Radi Cojbasic pour leurs commentaires et commentaires.

Au cours des deux dernières années, les STARK sont devenus une technologie clé et irremplaçable pour réaliser efficacement des preuves cryptographiques facilement vérifiables de déclarations très complexes (par exemple, prouver qu'un bloc Ethereum est valide). L'une des principales raisons en est la petite taille du champ : les SNARK basés sur des courbes elliptiques nécessitent de travailler sur des entiers de 256 bits pour être suffisamment sécurisés, tandis que les STARK vous permettent d'utiliser des tailles de champ beaucoup plus petites avec une plus grande efficacité : d'abord le champ Boucle d'or. (entier 64 bits), puis Mersenne 31 et BabyBear (tous deux 31 bits). En raison de cette efficacité gaiAinsi, Plonky 2 utilisant Boucle d'or est des centaines de fois plus rapide que ses prédécesseurs pour prouver de nombreux types de calculs.

Une question naturelle se pose : pouvons-nous pousser cette tendance jusqu’à sa conclusion logique et construire des systèmes de preuve qui fonctionnent plus rapidement en fonctionnant directement sur les zéros et les uns ? C’est exactement ce que Binius tente de faire, en utilisant un certain nombre d’astuces mathématiques qui le rendent très différent des SNARK et STARK d’il y a trois ans. Cet article décrit pourquoi les petits champs rendent la génération de preuves plus efficace, pourquoi les champs binaires sont particulièrement puissants et les astuces utilisées par Binius pour rendre les preuves sur les champs binaires si efficaces.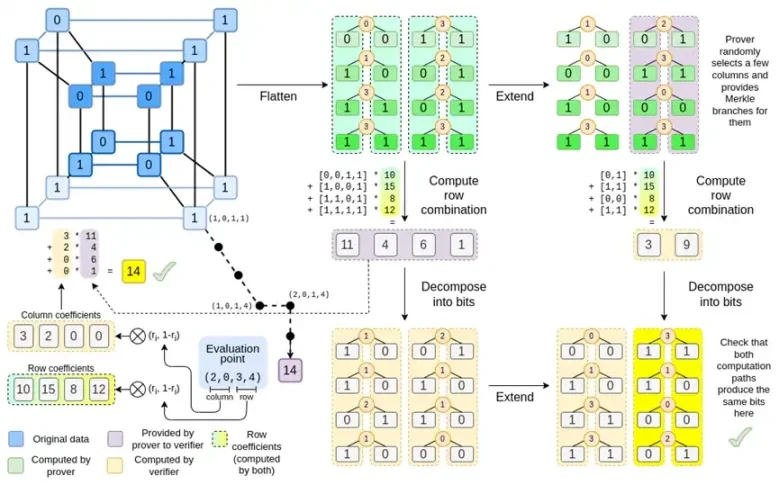

Binius, à la fin de cet article, vous devriez être capable de comprendre chaque partie de ce diagramme.

Révision : champs finis

L’une des tâches clés des systèmes de preuve cryptographique est de fonctionner sur de grandes quantités de données tout en limitant les chiffres. Si vous pouvez compresser une déclaration concernant un grand programme en une équation mathématique contenant quelques nombres, mais que ces nombres sont aussi grands que le programme d’origine, alors vous n’avez rien gagné.

Pour effectuer des calculs complexes tout en gardant des nombres petits, les cryptographes utilisent souvent l'arithmétique modulaire. On choisit un module premier p. L'opérateur % signifie prendre le reste : 15% 7 = 1, 53% 10 = 3, et ainsi de suite. (Notez que la réponse est toujours non négative, donc par exemple -1% 10 = 9)

Vous avez peut-être vu l'arithmétique modulaire dans le contexte de l'addition et de la soustraction de temps (par exemple, quelle heure est-il 9 heures après 4 ?). Mais ici, nous ne nous contentons pas d’ajouter et de soustraire modulo un nombre ; nous pouvons aussi multiplier, diviser et prendre des exposants.

Nous redéfinissons :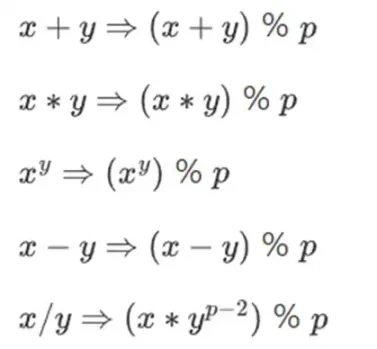

Les règles ci-dessus sont toutes cohérentes. Par exemple, si p = 7, alors :

5 + 3 = 1 (car 8% 7 = 1)

1-3 = 5 (car -2% 7 = 5)

2* 5 = 3

3/5 = 2

Un terme plus général pour de telles structures est celui de champs finis. Un corps fini est une structure mathématique qui suit les lois habituelles de l'arithmétique, mais dans laquelle le nombre de valeurs possibles est fini, de sorte que chaque valeur peut être représentée par une taille fixe.

L'arithmétique modulaire (ou champs premiers) est le type de corps fini le plus courant, mais il existe un autre type : les champs d'extension. Vous avez peut-être vu un champ d'extension : les nombres complexes. Nous imaginons un nouvel élément et l'étiquetons i, et faisons des calculs avec lui : (3i+2)*(2i+4)=6i*i+12i+4i+8=16i+2. Nous pouvons faire la même chose avec l’extension du champ premier. À mesure que nous commençons à traiter avec des champs plus petits, l'extension des champs premiers devient de plus en plus importante pour la sécurité, et les champs binaires (utilisés par Binius) dépendent entièrement de l'extension pour avoir une utilité pratique.

Révision : Arithmétisation

La manière dont les SNARK et les STARK prouvent les programmes informatiques se fait par l'arithmétique : vous prenez une déclaration sur le programme que vous souhaitez prouver et la transformez en une équation mathématique impliquant un polynôme. Une solution valide de l’équation correspond à une exécution valide du programme.

À titre d'exemple simple, supposons que j'ai calculé le 100e nombre de Fibonacci et que je veuille vous prouver de quoi il s'agit. Je crée un polynôme F qui code la séquence de Fibonacci : donc F(0)=F(1)=1, F(2)=2, F(3)=3, F(4)=5 et ainsi de suite pendant 100 pas . La condition que je dois prouver est que F(x+2)=F(x)+F(x+1) sur toute la plage x={0, 1…98}. Je peux vous convaincre en vous donnant le quotient :

où Z(x) = (x-0) * (x-1) * …(x-98). . Si je peux fournir que F et H satisfont cette équation, alors F doit satisfaire F(x+ 2)-F(x+ 1)-F(x) dans la plage. Si je vérifie en plus que pour F, F(0)=F(1)=1, alors F(100) doit en fait être le 100ème nombre de Fibonacci.

Si vous voulez prouver quelque chose de plus compliqué, alors vous remplacez la simple relation F(x+2) = F(x) + F(x+1) par une équation plus compliquée qui dit essentiellement que F(x+1) est la sortie d'initialiser une machine virtuelle avec l'état F(x), et exécuter une étape de calcul. Vous pouvez également remplacer le nombre 100 par un nombre plus grand, par exemple 1 000 000 000, pour permettre davantage d'étapes.

Tous les SNARK et STARK sont basés sur l'idée d'utiliser des équations simples sur des polynômes (et parfois des vecteurs et des matrices) pour représenter un grand nombre de relations entre des valeurs individuelles. Tous les algorithmes ne vérifient pas l'équivalence entre des étapes de calcul adjacentes comme ci-dessus : par exemple, PLONK ne le fait pas, et R1CS non plus. Mais bon nombre des contrôles les plus efficaces le font, car il est plus facile de minimiser les frais généraux en effectuant le même contrôle (ou les mêmes quelques contrôles) plusieurs fois.

Plonky 2 : Des SNARK et STARK 256 bits au 64 bits… uniquement des STARK

Il y a cinq ans, un résumé raisonnable des différents types de preuves de connaissance nulle était le suivant. Il existe deux types de preuves : les SNARK (basées sur une courbe elliptique) et les STARK (basées sur le hachage). Techniquement, les STARK sont un type de SNARK, mais en pratique, il est courant d'utiliser « SNARK » pour faire référence à la variante basée sur une courbe elliptique et « STARK » pour faire référence à la construction basée sur le hachage. Les SNARK sont petits, vous pouvez donc les vérifier très rapidement et les installer facilement en chaîne. Les STARK sont grands, mais ils ne nécessitent pas de configuration fiable et ils sont résistants aux quantiques.

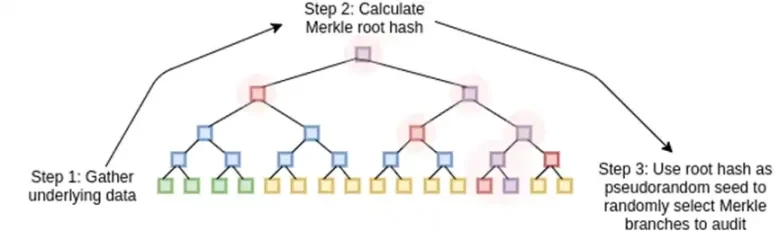
Les STARK fonctionnent en traitant les données comme un polynôme, en calculant le calcul de ce polynôme et en utilisant la racine de Merkle des données étendues comme « engagement polynomial ».

Un élément clé de l'histoire ici est que les SNARK basés sur des courbes elliptiques ont été largement utilisés en premier : les STARK ne sont devenus suffisamment efficaces que vers 2018, grâce à FRI, et à ce moment-là, Zcash fonctionnait depuis plus d'un an. Les SNARK basés sur une courbe elliptique ont une limitation clé : si vous souhaitez utiliser un SNARK basé sur une courbe elliptique, alors l'arithmétique dans ces équations doit être effectuée modulo le nombre de points sur la courbe elliptique. C'est un grand nombre, généralement proche de 2 à la puissance 256 : par exemple, pour la courbe bn128, c'est 21888242871839275222246405745257275088548364400416034343698204186575808495617. Mais l'informatique réelle utilise de petits nombres : si vous pensez sur un vrai programme dans votre langue préférée, la plupart des choses qu'il les utilisations sont des compteurs, des index dans les boucles for, des positions dans le programme, des bits uniques représentant vrai ou faux et d'autres éléments qui ne comportent presque toujours que quelques chiffres.

Même si vos données originales sont constituées de petits nombres, le processus de preuve nécessite le calcul de quotients, d'expansions, de combinaisons linéaires aléatoires et d'autres transformations de données qui entraîneront un nombre égal ou supérieur d'objets qui sont en moyenne aussi grands que la taille totale de votre champ. Cela crée une inefficacité clé : pour prouver un calcul sur n petites valeurs, vous devez effectuer beaucoup plus de calculs sur n valeurs beaucoup plus grandes. Initialement, les STARK ont hérité de l'habitude du SNARK d'utiliser des champs de 256 bits et ont donc souffert de la même inefficacité.

Développement de Reed-Solomon de certaines évaluations polynomiales. Même si la valeur d'origine est petite, les valeurs supplémentaires sont étendues à la taille totale du champ (dans ce cas 2^31 – 1)

En 2022, Plonky 2 est sorti. La principale innovation de Plonky 2 est de faire de l'arithmétique modulo un nombre premier plus petit : 2 à la puissance 64 – 2 à la puissance 32 + 1 = 18446744067414584321. Désormais, chaque addition ou multiplication peut toujours se faire en quelques instructions sur le CPU, et le hachage de toutes les données ensemble est 4 fois plus rapide qu'auparavant. Mais il y a un problème : cette méthode ne fonctionne que pour les STARK. Si vous essayez d'utiliser des SNARK, les courbes elliptiques deviennent peu sûres pour de si petites courbes elliptiques.

Pour garantir la sécurité, Plonky 2 doit également introduire des champs d'extension. Une technique clé pour vérifier les équations arithmétiques est l'échantillonnage aléatoire : si vous souhaitez vérifier si H(x) * Z(x) est égal à F(x+ 2)-F(x+ 1)-F(x), vous pouvez aléatoirement choisir une coordonnée r, fournir un engagement polynomial pour prouver H(r), Z(r), F(r), F(r+ 1) et F(r+ 2), puis vérifier si H(r) * Z(r ) est égal à F(r+ 2)-F(r+ 1)- F(r). Si un attaquant peut deviner les coordonnées à l’avance, il peut alors tromper le système de preuve – c’est pourquoi le système de preuve doit être aléatoire. Mais cela signifie également que les coordonnées doivent être échantillonnées à partir d’un ensemble suffisamment grand pour que l’attaquant ne puisse pas deviner au hasard. Ceci est évidemment vrai si le module est proche de 2 à la puissance 256. Cependant, pour le module 2^64 – 2^32 + 1, nous n’en sommes pas encore là, et ce n’est certainement pas le cas si l’on descend à 2 ^ 31 – 1. Il est tout à fait à la portée d'un attaquant d'essayer de forger une preuve deux milliards de fois jusqu'à ce qu'il ait de la chance.

Pour éviter cela, nous échantillonnons r à partir d'un champ étendu, afin que, par exemple, vous puissiez définir y où y^3 = 5 et prendre des combinaisons de 1, y et y^2. Cela porte le nombre total de coordonnées à environ 2^93. La plupart des polynômes calculés par le prouveur n'entrent pas dans ce domaine étendu ; ce ne sont que des entiers modulo 2 ^ 31-1, vous obtenez donc toujours toute l'efficacité de l'utilisation d'un petit champ. Mais les contrôles ponctuels aléatoires et les calculs FRI s’étendent à ce domaine plus vaste pour obtenir la sécurité dont ils ont besoin.

Des petits nombres premiers aux nombres binaires

Les ordinateurs font de l'arithmétique en représentant des nombres plus grands sous la forme de séquences de 0 et de 1, et en construisant des circuits au-dessus de ces bits pour calculer des opérations telles que l'addition et la multiplication. Les ordinateurs sont particulièrement optimisés pour les entiers de 16, 32 et 64 bits. Par exemple, 2^64 – 2^32 + 1 et 2^31 – 1 ont été choisis non seulement parce qu'ils s'inscrivent dans ces limites, mais aussi parce qu'ils s'inscrivent bien dans ces limites : multiplication modulo 2^64 – 2^32 + 1 peut être effectué en effectuant une multiplication régulière de 32 bits, en décalant et en copiant la sortie au niveau du bit à quelques endroits ; cet article explique bien certaines des astuces.

Cependant, une bien meilleure approche serait de faire les calculs directement en binaire. Et si l'addition pouvait être simplement XOR, sans avoir à se soucier du report de l'ajout de 1 + 1 d'un bit au suivant ? Et si la multiplication pouvait être davantage parallélisée de la même manière ? Ces avantages reposent tous sur la capacité de représenter des valeurs vraies/fausses avec un seul bit.

Obtenir ces avantages en effectuant directement du calcul binaire est exactement ce que Binius essaie de faire. L'équipe Binius a démontré les gains d'efficacité dans sa présentation au zkSummit :

Bien qu'elles soient à peu près de la même taille, les opérations sur les champs binaires 32 bits nécessitent 5 fois moins de ressources de calcul que les opérations sur les champs Mersenne 31 bits.

Des polynômes univariés aux hypercubes

Supposons que nous croyions à ce raisonnement et que nous voulions tout faire avec les bits (0 et 1). Comment représenter un milliard de bits avec un seul polynôme ?

Nous sommes ici confrontés à deux problèmes pratiques :

1. Pour qu'un polynôme représente un grand nombre de valeurs, ces valeurs doivent être accessibles lors de l'évaluation du polynôme : dans l'exemple de Fibonacci ci-dessus, F(0), F(1)… F(100), et dans un calcul plus large , les exposants seront en millions. Les champs que nous utilisons doivent contenir des nombres de cette taille.

2. Prouver n'importe quelle valeur que nous validons dans un arbre Merkle (comme tous les STARK) nécessite de l'encoder par Reed-Solomon : par exemple, étendre les valeurs de n à 8n, en utilisant la redondance pour empêcher les prouveurs malveillants de tricher en falsifiant une valeur pendant le calcul. Cela nécessite également d'avoir un champ suffisamment grand : pour passer d'un million de valeurs à 8 millions, il faut 8 millions de points différents pour évaluer le polynôme.

Une idée clé de Binius est de résoudre ces deux problèmes séparément, et ce en représentant les mêmes données de deux manières différentes. Premièrement, les polynômes eux-mêmes. Des systèmes tels que les SNARK basés sur des courbes elliptiques, les STARK de l'ère 2019, Plonky 2 et d'autres traitent généralement des polynômes sur une variable : F(x). Binius, quant à lui, s'inspire du protocole Spartan et utilise des polynômes multivariés : F(x 1, x 2,… xk). En effet, nous représentons l'intégralité de la trajectoire de calcul sur un hypercube de calcul, où chaque xi vaut 0 ou 1. Par exemple, si nous voulons représenter une séquence de Fibonacci, et que nous utilisons toujours un champ suffisamment grand pour les représenter, nous pouvons imaginez leurs 16 premières séquences comme ceci :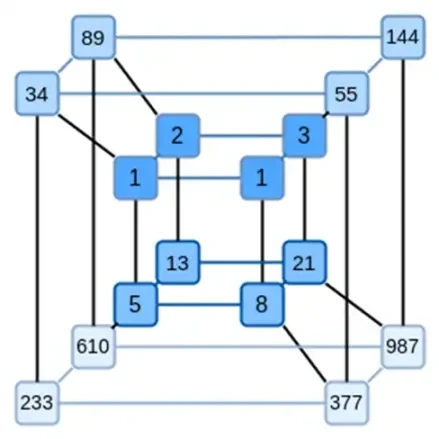

Autrement dit, F(0,0,0,0) devrait être 1, F(1,0,0,0) est également 1, F(0,1,0,0) est 2, et ainsi de suite, tous les jusqu'à F (1,1,1,1) = 987. Étant donné un tel hypercube de calculs, il existe un polynôme linéaire multivarié (degré 1 dans chaque variable) qui produit ces calculs. Nous pouvons donc considérer cet ensemble de valeurs comme représentant le polynôme ; nous n'avons pas besoin de calculer les coefficients.

Cet exemple n’est bien sûr qu’à titre d’illustration : en pratique, tout l’intérêt d’entrer dans l’hypercube est de nous permettre de traiter des bits individuels. La méthode native de Binius pour calculer les nombres de Fibonacci consiste à utiliser un cube de dimension supérieure, stockant un nombre par groupe de, disons, 16 bits. Cela nécessite une certaine ingéniosité pour implémenter l'addition d'entiers sur une base binaire, mais pour Binius, ce n'est pas trop difficile.

Examinons maintenant les codes d'effacement. La façon dont fonctionnent les STARK est que vous prenez n valeurs, Reed-Solomon les étend à plus de valeurs (généralement 8n, généralement entre 2n et 32n), puis sélectionnez au hasard certaines branches Merkle de l'expansion et effectuez une sorte de vérification sur elles. L'hypercube a une longueur de 2 dans chaque dimension. Par conséquent, il n’est pas pratique de l’étendre directement : il n’y a pas assez de place pour échantillonner des branches de Merkle à partir de 16 valeurs. Alors comment le fait-on? Supposons que l'hypercube soit un carré !

Binius simple – Un exemple

Voir ici pour une implémentation python du protocole.

Regardons un exemple, en utilisant des entiers réguliers comme champs pour plus de commodité (dans une implémentation réelle, nous utiliserions des éléments de champ binaires). Tout d’abord, nous codons l’hypercube que nous voulons soumettre sous forme de carré :

Maintenant, nous développons le carré en utilisant la méthode Reed-Solomon. Autrement dit, nous traitons chaque ligne comme un polynôme de degré 3 évalué à x = { 0, 1, 2, 3 } et évaluons le même polynôme à x = { 4, 5, 6, 7 } :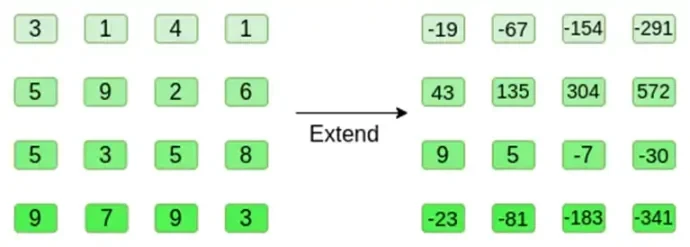

Notez que les chiffres peuvent devenir très importants ! C'est pourquoi, dans les implémentations pratiques, nous utilisons toujours des corps finis, plutôt que des entiers réguliers : si nous utilisons des entiers modulo 11, par exemple, le développement de la première ligne sera simplement [3, 10, 0, 6].

Si vous souhaitez essayer l'extension et vérifier les numéros vous-même, vous pouvez utiliser mon simple code d'extension Reed-Solomon ici.

Ensuite, nous traitons cette extension comme une colonne et créons un arbre Merkle de la colonne. La racine de l'arbre Merkle est notre engagement.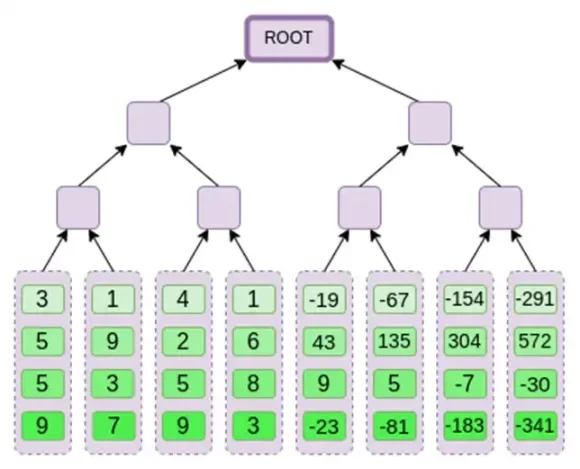

Supposons maintenant que le prouveur veuille prouver le calcul de ce polynôme r = {r 0, r 1, r 2, r 3 } à un moment donné. Il existe une différence subtile dans Binius qui le rend plus faible que les autres schémas d'engagement polynomial : le prouveur ne devrait pas connaître ou être capable de deviner s avant de s'engager sur la racine de Merkle (en d'autres termes, r devrait être une valeur pseudo-aléatoire qui dépend de la racine de Merkle). Cela rend le schéma inutile pour les recherches dans les bases de données (par exemple, ok, vous m'avez donné la racine Merkle, prouvez-moi maintenant P(0, 0, 1, 0) !). Mais les protocoles à preuve de connaissance nulle que nous utilisons réellement ne nécessitent généralement pas de recherche dans la base de données ; ils nécessitent uniquement de vérifier le polynôme à un point d'évaluation aléatoire. Cette restriction répond donc bien à nos objectifs.

Supposons que nous choisissions r = { 1, 2, 3, 4 } (le polynôme est évalué à -137 ; vous pouvez le confirmer en utilisant ce code). Passons maintenant à la preuve. Nous divisons r en deux parties : la première partie { 1, 2 } représente la combinaison linéaire des colonnes dans la ligne et la deuxième partie { 3, 4 } représente la combinaison linéaire des lignes. On calcule un produit tensoriel et pour les colonnes :

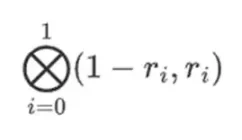
Pour la partie ligne :

Cela signifie : une liste de tous les produits possibles d’une valeur dans chaque ensemble. Dans le cas des lignes, on obtient :

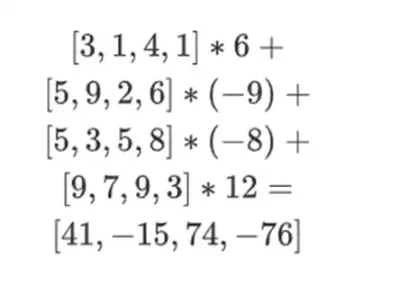
[( 1-r 2)*( 1-r 3), ( 1-r 3), ( 1-r 2)*r 3, r 2*r 3 ]

Avec r = { 1, 2, 3, 4 } (donc r 2 = 3 et r 3 = 4) :

[( 1-3)*( 1-4), 3*( 1-4),( 1-3)* 4, 3* 4 ] = [ 6, -9 -8 -12 ]

Maintenant, nous calculons une nouvelle ligne t en prenant une combinaison linéaire des lignes existantes. Autrement dit, nous prenons :

Vous pouvez considérer ce qui se passe ici comme une évaluation partielle. Si nous multipliions le produit tensoriel complet par le vecteur complet de toutes les valeurs, vous obtiendriez le calcul P(1, 2, 3, 4) = -137. Ici, nous avons multiplié le produit tensoriel partiel en utilisant seulement la moitié des coordonnées d'évaluation et réduit la grille de N valeurs à une seule ligne de N valeurs de racine carrée. Si vous donnez cette ligne à quelqu'un d'autre, il peut effectuer le reste du calcul en utilisant le produit tensoriel de l'autre moitié des coordonnées d'évaluation.

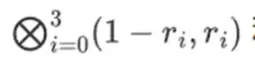
Le prouveur fournit au vérificateur la nouvelle ligne suivante : t et une preuve Merkle de certaines colonnes échantillonnées aléatoirement. Dans notre exemple illustratif, nous demanderons au prouveur de fournir uniquement la dernière colonne ; dans la vraie vie, le prouveur devrait fournir des dizaines de colonnes pour obtenir une sécurité adéquate.

Nous exploitons maintenant la linéarité des codes de Reed-Solomon. La propriété clé que nous exploitons est que prendre une combinaison linéaire de développements de Reed-Solomon donne le même résultat que prendre un développement de Reed-Solomon d'une combinaison linéaire. Cette indépendance séquentielle se produit généralement lorsque les deux opérations sont linéaires.

C’est exactement ce que fait le vérificateur. Ils calculent t et calculent des combinaisons linéaires des mêmes colonnes que celles calculées auparavant par le prouveur (mais uniquement les colonnes fournies par le prouveur) et vérifient que les deux procédures donnent la même réponse.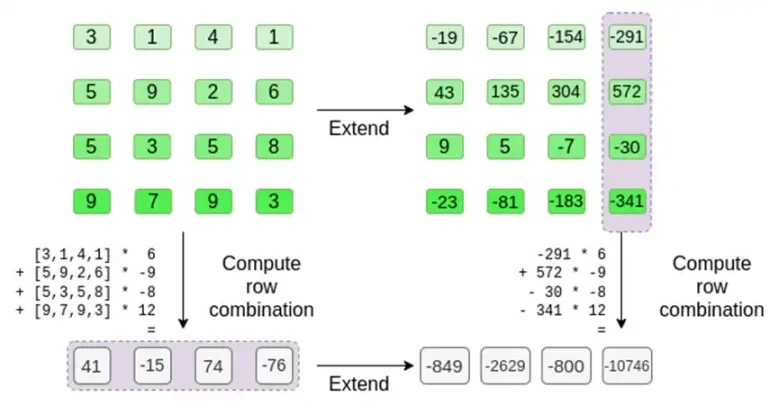

Dans ce cas, nous développons t et calculons la même combinaison linéaire ([6,-9,-8, 12]), qui donnent toutes deux la même réponse : -10746. Cela prouve que la racine de Merkle a été construite de bonne foi (ou du moins assez proche) et qu'elle correspond à t : au moins la grande majorité des colonnes sont compatibles entre elles.

Mais il y a encore une chose que le vérificateur doit vérifier : vérifier l'évaluation du polynôme {r 0 …r 3 }. Jusqu’à présent, toutes les étapes du vérificateur ne dépendaient pas réellement de la valeur revendiquée par le prouveur. Voici comment nous le vérifions. On prend le produit tensoriel de la « partie colonne » que l’on a marqué comme point de calcul :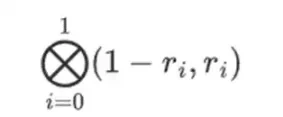

Dans notre cas, où r = { 1, 2, 3, 4 } donc la moitié des colonnes sélectionnées est { 1, 2 }), cela équivaut à :

Prenons maintenant cette combinaison linéaire t :

Cela revient à résoudre directement le polynôme.

Ce qui précède est très proche d’une description complète du simple protocole Binius. Cela présente déjà des avantages intéressants : par exemple, puisque les données sont séparées en lignes et en colonnes, vous n'avez besoin que d'un champ deux fois plus petit. Cependant, cela ne permet pas d’obtenir tous les avantages de l’informatique binaire. Pour cela, nous avons besoin du protocole Binius complet. Mais d’abord, examinons de plus près les champs binaires.

Champs binaires

Le plus petit champ possible est l'arithmétique modulo 2, qui est si petit que l'on peut lui écrire des tables d'addition et de multiplication :

Nous pouvons obtenir des champs binaires plus grands par extension : si nous commençons par F 2 (entiers modulo 2) puis définissons x où x au carré = x + 1 , nous obtenons les tables d'addition et de multiplication suivantes :

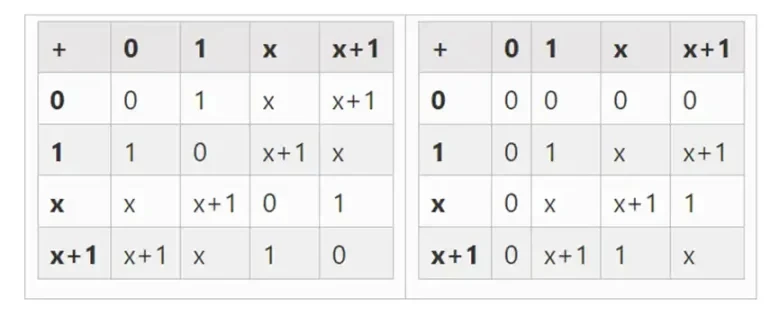
Il s’avère que nous pouvons étendre les champs binaires à des tailles arbitrairement grandes en répétant cette construction. Contrairement aux nombres complexes sur les nombres réels, où vous pouvez ajouter un nouvel élément mais ne jamais ajouter d'autres éléments I (les quaternions existent, mais ils sont mathématiquement étranges, par exemple ab n'est pas égal à ba), avec des champs finis, vous pouvez ajouter de nouvelles extensions. pour toujours. Plus précisément, notre définition d'un élément est la suivante :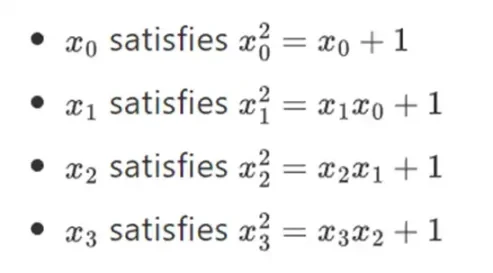

Et ainsi de suite… C'est ce qu'on appelle souvent la construction d'une tour, car chaque expansion successive peut être considérée comme l'ajout d'une nouvelle couche à la tour. Ce n'est pas la seule façon de construire des champs binaires de taille arbitraire, mais cela présente des avantages uniques que Binius exploite.

Nous pouvons représenter ces nombres sous forme de listes de bits. Par exemple, 1100101010001111. Le premier bit représente des multiples de 1, le deuxième bit représente des multiples de x0, puis les bits suivants représentent des multiples de x1 : x1, x1*x0, x2, x2*x0, et ainsi de suite. Cet encodage est sympa car vous pouvez le décomposer :

Il s'agit d'une notation relativement rare, mais j'aime représenter les éléments de champ binaires sous forme d'entiers, avec le bit le plus efficace à droite. Autrement dit, 1 = 1, x0 = 01 = 2, 1+x0 = 11 = 3, 1+x0+x2 = 11001000 = 19, et ainsi de suite. Dans cette représentation, c'est 61779.

L'addition dans le champ binaire n'est qu'un XOR (tout comme la soustraction, d'ailleurs) ; notez que cela signifie x+x = 0 pour tout x. Pour multiplier deux éléments x*y ensemble, il existe un algorithme récursif très simple : diviser chaque nombre en deux :

Ensuite, divisez la multiplication :

La dernière partie est la seule qui est un peu délicate, car il faut appliquer des règles de simplification. Il existe des moyens plus efficaces de faire la multiplication, similaires à l'algorithme de Karatsubas et aux transformations rapides de Fourier, mais je laisserai cela comme un exercice au lecteur intéressé.

La division dans les corps binaires se fait en combinant multiplication et inversion. La méthode d'inversion simple mais lente est une application du petit théorème de Fermats généralisé. Il existe également un algorithme d'inversion plus complexe mais plus efficace que vous pouvez trouver ici. Vous pouvez utiliser le code ici pour jouer avec l'addition, la multiplication et la division de champs binaires.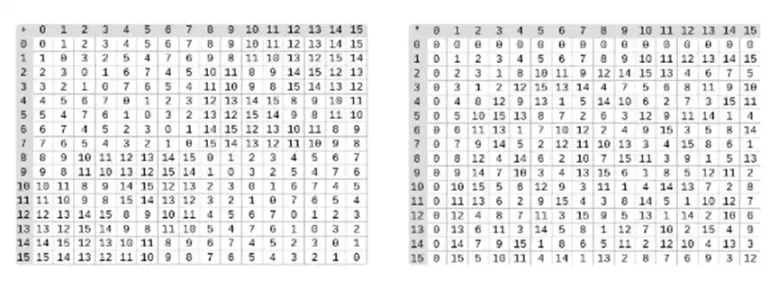

À gauche : table d'addition pour les éléments de champ binaires à quatre bits (c'est-à-dire uniquement 1, x 0, x 1, x 0x 1). À droite : table de multiplication pour les éléments de champ binaires à quatre bits.

La beauté de ce type de champ binaire est qu’il combine certains des meilleurs éléments des entiers réguliers et de l’arithmétique modulaire. Comme les entiers normaux, les éléments de champ binaires ne sont pas limités : vous pouvez les agrandir autant que vous le souhaitez. Mais tout comme l’arithmétique modulaire, si vous opérez sur des valeurs comprises dans une certaine limite de taille, tous vos résultats resteront dans la même plage. Par exemple, si vous portez 42 aux puissances successives, vous obtenez :

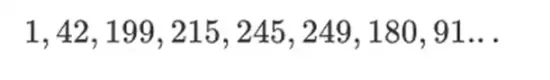
Après 255 étapes, vous revenez à 42 à la puissance 255 = 1, et tout comme les entiers positifs et les opérations modulaires, ils obéissent aux lois habituelles des mathématiques : a*b=b*a, a*(b+c)= a*b+a*c, et même de nouvelles lois étranges.

Enfin, les champs binaires sont pratiques pour manipuler des bits : si vous faites des mathématiques avec des nombres qui tiennent dans 2 000 bits, alors toute votre sortie tiendra également dans 2 000 bits. Cela évite la gêne. Dans Ethereums EIP-4844, les blocs individuels d'un blob doivent être des nombres modulo 52435875175126190479447740508185965837690552500527637822603658699938581184513, donc le codage des données binaires nécessite de perdre de l'espace et d'effectuer des vérifications supplémentaires au niveau de la couche application. pour garantir que la valeur stockée dans chaque élément est inférieure à 2248. Ceci Cela signifie également que les opérations sur le terrain binaire sont ultra rapides sur les ordinateurs – à la fois sur les processeurs et sur les conceptions FPGA et ASIC théoriquement optimales.

Tout cela signifie que nous pouvons effectuer un codage Reed-Solomon comme nous l'avons fait ci-dessus, d'une manière qui évite complètement l'explosion d'entiers comme nous l'avons vu dans notre exemple, et d'une manière très native, le type de calculs pour lesquels les ordinateurs sont doués. La propriété split des champs binaires – comment faire 1100101010001111 = 11001010 + 10001111*x 3 , puis le diviser selon nos besoins – est également cruciale pour permettre une grande flexibilité.

Terminer Binius

Voir ici pour une implémentation python du protocole.

Nous pouvons maintenant passer au « Binius complet », qui adapte le « Binius simple » pour (i) travailler sur des champs binaires et (ii) valider des bits uniques. Ce protocole est difficile à comprendre car il alterne entre différentes manières d'examiner les matrices de bits ; il m’a certainement fallu plus de temps pour le comprendre qu’il ne me faut habituellement pour comprendre les protocoles cryptographiques. Mais une fois que vous comprenez les champs binaires, la bonne nouvelle est que les « mathématiques plus difficiles » sur lesquelles s'appuie Binius n'existent pas. Il ne s’agit pas d’appariements de courbes elliptiques, où il y a des trous de lapin de géométrie algébrique de plus en plus profonds à descendre ; ici, vous n'avez que des champs binaires.

Regardons à nouveau le tableau complet :

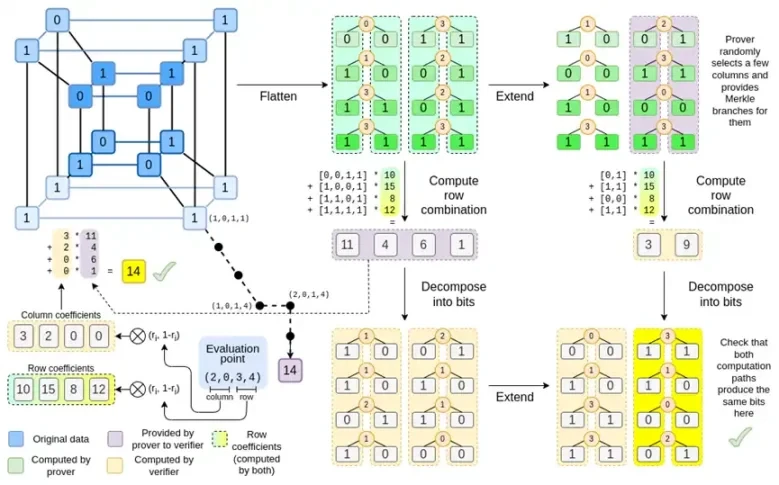
À présent, vous devriez être familier avec la plupart des composants. L'idée d'aplatir un hypercube dans une grille, l'idée de calculer des combinaisons de lignes et de colonnes en tant que produits tensoriels de points d'évaluation, et l'idée de vérifier l'équivalence entre l'expansion de Reed-Solomon puis le calcul des combinaisons de lignes et le calcul des combinaisons de lignes puis l'expansion de Reed-Solomon sont tous implémentés dans Binius simple.

Quoi de neuf dans Complete Binius ? En gros trois choses :

• Les valeurs individuelles dans l'hypercube et le carré doivent être des bits (0 ou 1).

• Le processus d'expansion étend les bits en davantage de bits en les regroupant en colonnes et en supposant temporairement qu'ils constituent des éléments d'un champ plus grand.

• Après l'étape de combinaison de lignes, il y a une étape de décomposition élément par élément en bits qui reconvertit l'expansion en bits.

Eh bien, discutons des deux cas tour à tour. Tout d’abord, la nouvelle procédure de prolongation. Les codes Reed-Solomon ont une limitation fondamentale, si vous souhaitez étendre n à k*n, vous devez travailler dans un champ avec k*n valeurs différentes qui peuvent être utilisées comme coordonnées. Avec F 2 (alias bits), vous ne pouvez pas faire ça. Ce que nous faisons donc, c'est regrouper les éléments adjacents de F 2 pour former des valeurs plus grandes. Dans l'exemple ici, nous emballons deux bits à la fois dans les éléments { 0 , 1 , 2 , 3 } , ce qui nous suffit puisque notre extension n'a que quatre points de calcul. Dans une vraie preuve, nous pourrions revenir en arrière 16 bits à la fois. Nous exécutons ensuite le code Reed-Solomon sur ces valeurs compressées et les décompactons à nouveau en bits.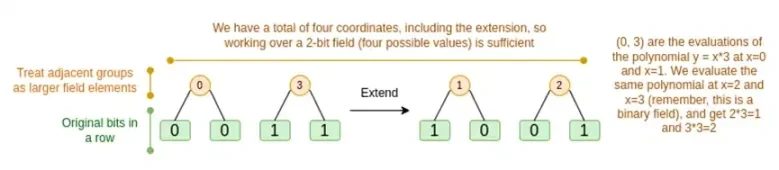

Maintenant, les combinaisons de lignes. Afin de rendre l'évaluation à un point aléatoire sécurisée cryptographiquement, nous devons échantillonner ce point à partir d'un espace assez grand (beaucoup plus grand que l'hypercube lui-même). Ainsi, même si le point à l’intérieur de l’hypercube est le bit, la valeur calculée à l’extérieur de l’hypercube sera beaucoup plus grande. Dans l'exemple ci-dessus, la combinaison de lignes finit par être [11, 4, 6, 1].

Cela pose un problème : nous savons comment regrouper des bits en une valeur plus grande, puis effectuer une expansion de Reed-Solomon sur cette valeur, mais comment faire la même chose pour des paires de valeurs plus grandes ?

L'astuce de Binius consiste à le faire petit à petit : nous examinons un seul bit de chaque valeur (par exemple, pour la chose que nous avons étiquetée 11, c'est [1, 1, 0, 1]), puis nous le développons ligne par ligne. Autrement dit, nous l'étendons sur la ligne 1 de chaque élément, puis sur la ligne x0, puis sur la ligne x1, puis sur la ligne x0x1, et ainsi de suite (enfin, dans notre exemple de jouet, nous nous arrêtons là, mais dans un vrai l'implémentation ira jusqu'à 128 lignes (la dernière étant x6***…*x0))

revoir:

• Nous convertissons les bits de l'hypercube en une grille

• Nous traitons ensuite les groupes de bits adjacents sur chaque ligne comme des éléments d'un champ plus grand et effectuons des opérations arithmétiques sur eux pour que Reed-Solomon agrandisse la ligne.

• Nous prenons ensuite la combinaison de lignes de chaque colonne de bits et obtenons la colonne de bits pour chaque ligne en sortie (beaucoup plus petite pour les carrés de plus de 4 x 4)

• Ensuite, nous considérons la sortie comme une matrice et ses bits comme des lignes

Pourquoi cela arrive-t-il? En mathématiques normales, si vous commencez à découper un nombre petit à petit, la capacité (habituelle) d'effectuer des opérations linéaires dans n'importe quel ordre et d'obtenir le même résultat s'effondre. Par exemple, si je commence par le nombre 345, et que je le multiplie par 8, puis par 3, j'obtiens 8280, et si je fais ces deux opérations à l'envers, j'obtiens aussi 8280. Mais si j'insère une opération de découpage en bits entre les deux étapes, ça se décompose : si tu fais 8x, puis 3x, tu obtiens :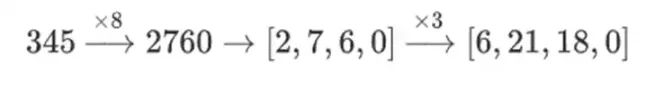

Mais si vous faites 3x, puis 8x, vous obtenez :

Mais dans les champs binaires construits avec des structures en tour, cette approche fonctionne. La raison en est leur séparabilité : si vous multipliez une grande valeur par une petite valeur, ce qui se passe sur chaque segment reste sur chaque segment. Si nous multiplions 1100101010001111 par 11, cela équivaut à la première décomposition de 1100101010001111, qui est

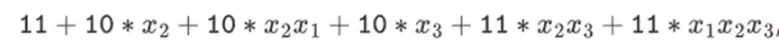
Multipliez ensuite chaque composant par 11.

Mettre tous ensemble

En général, les systèmes de preuve sans connaissance fonctionnent en faisant des déclarations sur un polynôme qui représentent en même temps des déclarations sur l'évaluation sous-jacente : tout comme nous l'avons vu dans l'exemple de Fibonacci, F(X+ 2)-F(X+ 1)-F( X) = Z(X)*H(X) en vérifiant toutes les étapes du calcul de Fibonacci. Nous vérifions les affirmations sur le polynôme en prouvant l'évaluation à des points aléatoires. Cette vérification de points aléatoires représente une vérification de l'ensemble du polynôme : si l'équation du polynôme ne correspond pas, il y a une petite chance qu'elle corresponde à une coordonnée aléatoire spécifique.

En pratique, une source majeure d'inefficacité est que dans les programmes réels, la plupart des nombres que nous traitons sont petits : indices dans les boucles for, valeurs Vrai/Faux, compteurs, etc. Cependant, lorsque nous étendons les données avec le codage Reed-Solomon pour fournir la redondance requise pour sécuriser les contrôles basés sur Merkle, la plupart des valeurs supplémentaires finissent par occuper toute la taille du champ, même si la valeur d'origine était petite.

Pour résoudre ce problème, nous souhaitons rendre ce champ aussi petit que possible. Plonky 2 nous a fait passer de nombres de 256 bits à des nombres de 64 bits, puis Plonky 3 l'a encore réduit à 31 bits. Mais même cela n’est pas optimal. Avec les champs binaires, nous pouvons traiter des bits uniques. Cela rend le codage dense : si vos données sous-jacentes réelles ont n bits, alors votre codage aura n bits et l'expansion aura 8*n bits, sans surcharge supplémentaire.

Maintenant, regardons ce graphique une troisième fois :

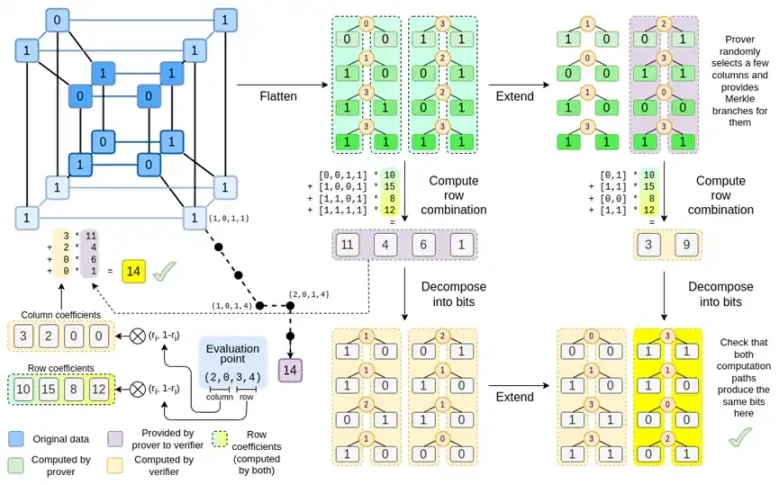
Dans Binius, nous travaillons sur un polynôme multilinéaire : un hypercube P(x0, x1,…xk) où les évaluations uniques P(0, 0, 0, 0), P(0, 0, 0, 1) jusqu'à P( 1, 1, 1, 1), contiennent les données qui nous intéressent. Pour prouver un calcul à un certain point, nous réinterprétons les mêmes données sous forme de carré. Nous étendons ensuite chaque ligne, en utilisant le codage Reed-Solomon pour fournir la redondance des données requise pour la sécurité contre les requêtes aléatoires de branche Merkle. Nous calculons ensuite des combinaisons linéaires aléatoires des lignes, en concevant les coefficients de manière à ce que la nouvelle ligne combinée contienne réellement la valeur calculée qui nous intéresse. Cette ligne nouvellement créée (réinterprétée comme une ligne de 128 bits) et certaines colonnes sélectionnées au hasard avec des branches Merkle sont transmises au vérificateur.

Le vérificateur effectue ensuite la combinaison de lignes étendues (ou plus précisément, les colonnes étendues) et la combinaison de lignes étendues et vérifie que les deux correspondent. Il calcule ensuite une combinaison de colonnes et vérifie qu'elle renvoie la valeur revendiquée par le prouveur. Il s'agit de notre système de preuve (ou plus précisément, du schéma d'engagement polynomial, qui est un élément clé du système de preuve).

Qu’est-ce que nous n’avons pas encore abordé ?

• Un algorithme efficace pour étendre les lignes est nécessaire pour rendre le validateur efficace sur le plan informatique. Nous utilisons la transformation de Fourier rapide sur les champs binaires, décrite ici (bien que l'implémentation exacte soit différente, car cet article utilise une construction moins efficace qui n'est pas basée sur une expansion récursive).

• Arithmétiquement. Les polynômes univariés sont pratiques car vous pouvez faire des choses comme F(X+2)-F(X+1)-F(X) = Z(X)*H(X) pour lier des étapes adjacentes dans le calcul. Dans l’hypercube, l’étape suivante est beaucoup moins bien expliquée que X+1. Vous pouvez faire X+k, puissances de k, mais ce comportement de saut sacrifie de nombreux avantages clés de Binius. L'article de Binius décrit la solution. Voir la section 4.3), mais il s’agit là d’un profond terrier de lapin en soi.

• Comment effectuer en toute sécurité des contrôles de valeurs spécifiques. L'exemple de Fibonacci nécessitait de vérifier les conditions aux limites clés : les valeurs de F(0)=F(1)=1 et F(100). Mais pour Binius original, il n'est pas sûr d'effectuer des vérifications à des points de calcul connus. Il existe des moyens assez simples de convertir des contrôles de calcul connus en contrôles de calcul inconnus, en utilisant ce que l'on appelle des protocoles de vérification de somme ; mais nous ne les aborderons pas ici.

• Les protocoles de recherche, une autre technologie largement utilisée récemment, sont utilisés pour créer des systèmes de preuve extrêmement efficaces. Binius peut être utilisé conjointement avec des protocoles de recherche pour de nombreuses applications.

• Au-delà du temps de vérification de la racine carrée. Les racines carrées coûtent cher : une preuve Binius de 2 ^ 32 bits fait environ 11 Mo de long. Vous pouvez compenser cela en utilisant d'autres systèmes de preuves pour réaliser des preuves de preuves Binius, vous offrant ainsi l'efficacité d'une preuve Binius avec une taille de preuve plus petite. Une autre option est le protocole FRI-Binius, plus complexe, qui crée une preuve de taille multi-logarithmique (tout comme le FRI classique).

• Comment Binius affecte la convivialité de SNARK. Le résumé de base est que si vous utilisez Binius, vous n'avez plus à vous soucier de rendre les calculs arithmétiquement amicaux : le hachage régulier n'est plus plus efficace que le hachage arithmétique traditionnel, la multiplication modulo 2 à la puissance 32 ou modulo 2 à la puissance 32. 256 n'est plus aussi pénible que la multiplication modulo 2, etc. Mais c'est un sujet complexe. Beaucoup de choses changent lorsque tout est fait en binaire.

Je m'attends à voir davantage d'améliorations dans la technologie de preuve basée sur les champs binaires dans les mois à venir.

Cet article provient d'Internet : Vitalik : Binius, des preuves efficaces pour les champs binaires

En relation: La pièce BNB montre des signes de reprise : un nouveau record annuel en vue

En bref Le prix du BNB a rebondi de $550 pour se rapprocher de la rupture de la résistance $593. Les indicateurs de prix ont retrouvé leur dynamique haussière, ce qui soutient une hausse de 8%. Le ratio Sharpe de 4,03 incitera probablement de nouveaux investisseurs à se tourner vers le jeton d'échange. Mars a été un mois favorable pour BNB Coin, la crypto-monnaie atteignant deux nouveaux sommets annuels en quelques jours seulement avant de connaître une correction. Après une période de reprise de près de deux semaines, BNB Coin montre des signes d’atteinte potentielle d’un nouveau sommet en 2024. Mais une telle étape est-elle réalisable ? BNB semble prometteur Suite à un rebond par rapport au niveau de support $550, la valeur de BNB Coin a augmenté à $581 au moment de cette analyse. Cette amélioration reflète une reprise du profil risque-rendement de l'altcoin,…